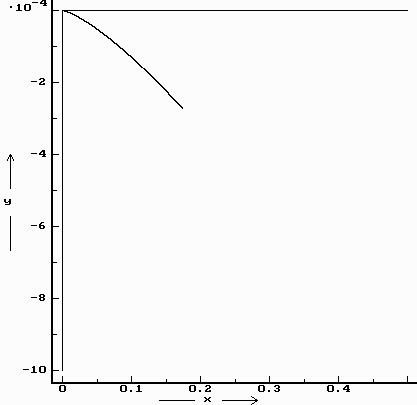Fyzikální seminář FJFI ČVUT 1998/1999
Studenti soběVolný pád na rotující Zemi
Jan Mužík
(MUZIK@ KM1.FJFI.CVUT.CZ)
Tycho de Brahe argumentoval proti rotaci Země tím, že na rotující Zemi by kámen puštěný z vysoké věže nemohl spadnout kolmo k jejímu úpatí
.Dnes samozřejmě víme, že Země skutečně rotuje, a protože Brahova argumentace byla logicky správná, budeme tedy hledat, jak se těleso, volně puštěné z výšky
h , odchýlí od úpatí věže, proč se vlastně od úpatí odchyluje (jaké síly ho k tomu ‘nutí’ a proč de Brahe argumentoval něčím, co tedy v podstatě existuje.Nejprve si musíme uvědomit, že rotace Země je dnes již nepopiratelný fakt. V našem běžném životě však vše automaticky spojujeme s ‘pevnou’ Zemí a její rotace si nejsme v podstatě vědomi. Budeme-li chtít i nadále používat tuto soustavu (spojenou s pevnou Zemí), musíme počítat s tím, že ve své podstatě je to tedy soustava
neinerciální (pohybuje se se zrychlením a existují v ní tzv. setrvačné nepravé síly).Zvolíme-li počátek soustavy souřadnic ve středu Země a osy pevně spojíme s rotující Zemí, z teorie potom vyplyne tato pohybová rovnice na povrchu Země:
![]()
První člen na pravé straně představuje jedinou uvažovanou pravou sílu (gravitační působení Země).
Druhý člen vyjadřuje setrvačnou sílu způsobenou nerovnoměrností translačního pohybu Země na její dráze. Nerovnoměrnost je dána druhým Keplerovým zákonem, činí cca 1
o za den, a proto ji můžeme zanedbat.Třetí člen vyjadřuje Eulerovu sílu, která by se projevila při zpomalování nebo zrychlování zemské rotace. Tyto změny jsou však zcela zanedbatelné.
Čtvrtý člen je síla odstředivá, míří kolmo od zemské osy. Tato síla se vektorově sčítá se silou gravitační na sílu tíhovou.
Poslední síla vystupující na pravé straně je síla Coriolisova.
N
yní můžeme tedy napsat pohybovou rovnici pro zrychlení na povrchu Země ve tvaru: ( v - rychlost vůči rotující Zemi, w - úhlová rychlost rotace Země )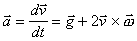
Prostudujeme tedy nyní vliv Coriolisovy síly na volný pád na rotující Zemi. Soustavu souřadnic přitom zvolíme ve vybraném místě zemského povrchu o zeměpisné šířce j
, osu z svisle vzhůru, osu x na východ a osu y na sever.Vektory tedy budou:
![]()
A pohybovou rovnici můžeme rozepsat:
a
= (0,0,-g) + 2(vyw z - vzw y, vzw x - vxw z, vxw y - vyw x)a=(0,0,-g)+2(y· w sinj - z· w cosj , z· 0 - x· w sinj , x· w cosj - y· 0)
a=( 2y· w sinj - 2z· w cosj , - 2x· w sinj , 2x· w cosj - g )
·
x· = 2y· w sinj - 2z· w cosj·
y· = - 2x· w sinj·
z· = 2x· w cosj - gRovnice integrujeme na:
x· = 2yw sinj - 2zw cosj + C1
y· = - 2xw sinj + C2
z· = 2xw cosj - gt + C3
Při počátečních podmínkách:
t = 0, x = y = 0, z = h, x· = y· = z· = 0Þ C1 = 2hw cosj
C2 = 0
C2 = 0
Rovnice pro x· , y· , z· dosadíme do rovnic pro · x· , · y· , · z· .
·
x· = -4xw 2sin2j - 4xw 2cos2j + 2w cosj gt·
y· = - 4yw 2sin2j + 4zw 2sinj cosj - 4hw 2sinj cosj·
z· = 4yw 2sinj cosj -4zw 2cos2j + 4hw 2cos2j - gJelikož je w
= 7,27 10-5 dosti malé, můžeme členy druhého řádu obsahující w 2 zanedbat. V tomto přiblížení dostáváme v souhlase s počátečními podmínkami:1.)
integrací: x· = 2w cosj (1/2)gt2 = w cosj gt2 + C (C=0)x = gw cosj (1/3)t3 =
y = 0
z· = -gt + C (C=0)
z = -(1/2)gt2 + C (C=h)
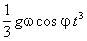
y = 0
z = 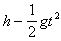
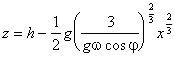
Pro z = 0 dostanem
e odchylku dopadu tělesa od paty kolmice: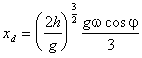
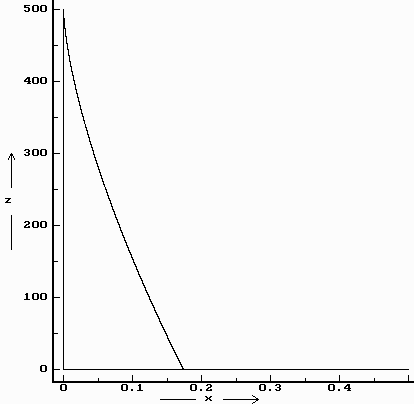
Toto je semikubická (Neilova) parabola. (Graf 1)
Máme tedy první přibližný, i když pro pozemské možnosti dostatečně přesný výsledek.
Zkusme nyní integrovat rovnice · x· , · y· , · z· ,
aniž bychom členy w 2 zanedbávali. Dostaneme tím zcela přesné výsledky.2.)
integr. x· =-4xw 2sin2j t -4xw 2cos2j t + 2w cosj g(1/2)t2 +C1x=-2xw 2sin2j t2 -2xw 2cos2j t2 + w cosj g(1/3)t3 +C2
C1=0 C2=0
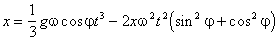
x(1+2w 2t2)=(1/3)gw cosj
t3 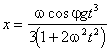 R1
R1
y· =-4yw 2sin2j t + 2zw 2sin(2j )t - 2hw 2sin(2j )t + C3
y =-2yw 2sin2j t2 + zw 2sin(2j )t2 - hw 2sin(2j )t2 + C4
C3=0 C4=0
y(1+2w 2sin2j t2)=w 2sin(2j )t2(z-h)
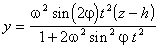 R2
R2
z·
=2yw 2sin(2j )t - 4zw 2cos2j t + 4hw 2cos2j t -gt + C5z=yw 2sin(2j )t2-2zw 2cos2j t2+2hw 2cos2j t2-(1/2)gt2+C6
C5=0 C6=h
z(1+2w 2cos2j t2)=yw 2sin(2j )t2+2hw 2cos2j t2+h-(1/2)gt2
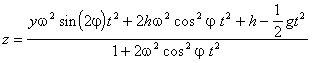 R3
R3
Dostáváme soustavu tří rovnic (R1, R2, R3) závislých na parametru
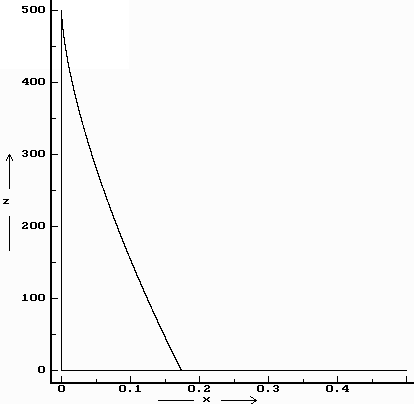
t , čas bychom mohli vyjádřit a dosadit, dostali bychom rovnici prostorové trajektorie, ale tuto operaci se mi nepodařilo ‘slušně’ provést.Namodeloval jsem tedy alespoň příslušné průběhy v programu Famulus (viz.Grafy).
Už z rovnic můžeme vyčíst, že těleso bude, v souhlase s předchozím výpočtem, uchylováno do kladné části osy
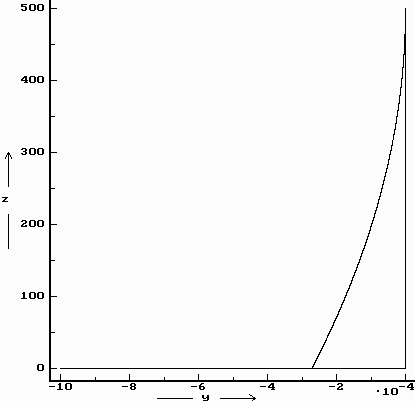
x (tj. na východ).Je ovšem možné také vidět, že těleso bude též uchylováno do záporné části osy
y (tj. na jih). Jak moc není zřejmé, ale díky namodelování vidíme, že tato výchylka je velice malá, v skutku zanedbatelná. Pád k ose y je též po semikubické (Neilově) parabole (viz graf).Posledním z grafů je křivka mezi osami
x a y . Je to v podstatě pohled na rovinu dopadu, kdy osa z jde jako by k nám.Takto jsme tedy získali odchylky pomocí počítání setrvačných (konkr. Coriolisovy) sil v neinerciální rotující soustavě pevně spojené se Zemí.
Tentýž výsledek bychom museli dostat při výpočtu v inerciální soustavě v níž Země rotuje. Pak by se Coriolisova síla neuplatnila, ale museli bychom vzít v úvahu, že dokud je těleso ve
výšce h nad Zemí, pohybuje se tečnou rychlostí vh=(RZ+h)w , zatímco úpatí pod touto výškou jen v0=RZw . Jde tedy o vodorovný vrh nad pohybující se základnou.Jakmile těleso z výšky
h pustíme, začne na ně působit vodorovná složka tíhové síly, která jeho pohyb ve směru osy x dále ovlivňuje. Protože h< < RZ můžeme přibližně psát pro zrychlení ve směru osy x :Dosadíme-li za t dobu volného pádu 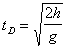

Pokud by pokus probíhal v zeměpisné šířce j , nahradili bychom vždy úhlovou rychlost w
její projekcí w cosj .
Zjistili jsme tedy, že při volném pádu na rotující zemi se volně puštěné těleso opravdu odchyluje, tato odchylka je však dosti malá, a proto v praxi prakticky nepozorovatelná. Proto tedy asi Tycho de Brahe argumentoval něčím, co ve své podstatě existuje.
Tuto odchylku můžeme vysvětlit buďto v neinerciální soustavě pomocí Coriolisovy síly, a nebo v inerciální soustavě pomocí faktu, že při stejné úhlové rychlosti w je na větším poloměru větší obvodová rychlost.
Obrázky: