Doplňkový text k přednášce o chaosu

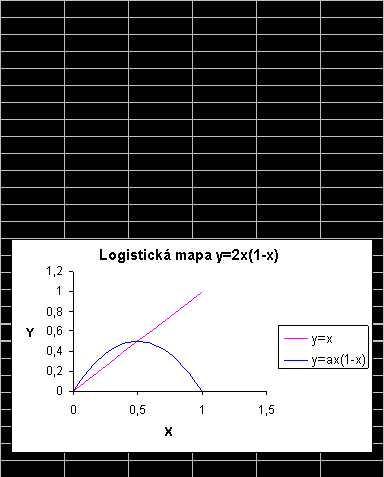
Jsou charakterizovány vztahem g(x)=ax(1-x), kde konstanta a vyjadřuje vlastnosti popisovaného systému a člen (1-x) závislost na nepostradatelných zdrojích. Vhodným příkladem je třeba rybník. Zde konstanta a vyjadřuje především reprodukční schopnost daného druhu ryb a člen (1-x) je závislost na potravě.

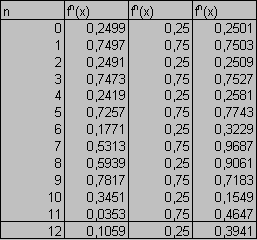
Je-li nějaký dynamický systém popsán funkcí (logistickou mapou) g(x) a na počátku se nachází ve stavu x, potom x nazveme počáteční podmínkou a g(x) novým stavem dynamického systému, do kterého po čase přejde. Tento stav je ovšem zároveň počáteční podmínkou pro další vývoj dynamického systému a po čase přejde do stavu g(g(x)). Proto zavedu

Graf 1 obsahuje dva velmi zajímavé body. Jsou to průsečíky grafu y=x a y=2x(1-x). První z nich je v počátku a jeho zvláštností je, že pro všechny počáteční podmínky x v okolí bodu 0 se gⁿ(x) od nuly vzdaluje. Takový bod se nazývá zdroj (source). Druhý průsečík naproti tomu vykazuje opačné vlastnosti. gⁿ(x) se pro všechny počáteční podmínky v okolí bodu 0,5 k tomuto bodu blíží a nakonec se na něm ustálí. Takový bod se nazývá kanál (sink). Určování maximálních okolí zdrojů a kanálů, pro která si tyto body zachovávají své vlastnosti, je těžké a záleží vždy na dané logistické mapě.

Pro g(x)=2x(1-x) platí: n je přirozené číslo

- počáteční podmínky x je z intervalu (0;0,5) gⁿ(x) jde k 0,5

(0,5;1) g(x) je z intervalu (0;0,5) a gⁿ(x) jde k 0,5

x<0 gⁿ(x) jde k mínus nekonečnu

x>1 g(x)<0 a gⁿ(x) jde k mínus nekonečnu

x=0 gⁿ(x)=0

x=0,5 gⁿ(x)=0,5

x=1 gⁿ(x)=0

Chování je zřejmé z následující tabulky.

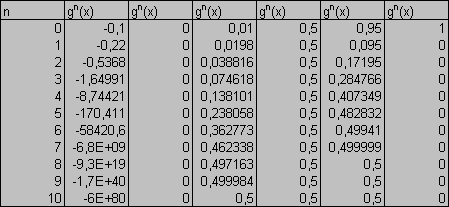
Pro vyšší hodnoty konstanty a začnou logistické mapy vykazovat stále větší chaos.

Pokud je a=3,3, tak se objeví další zvláštnost. V grafu jsou dva body (nejsou to průsečíky), mezi kterými začne mapa g(x) alternovat. Stane se tak pro jakoukoliv počáteční podmínku x z intervalu (0;1) mimo 0,6969...

Tabulka 2

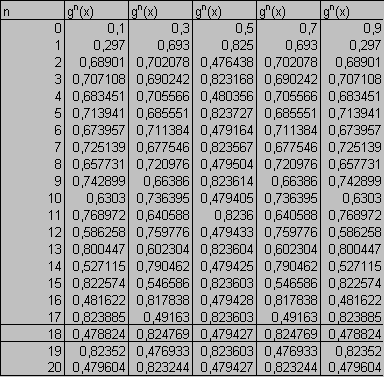
U takových map říkáme, že mají dvou bodový kanál. Spolu s rostoucí konstantou a mají kanály více bodů. Abychom měli lepší představu o tom, jak se logistické mapy chovají, kreslí se tzv. bifurkační mapy. V takovém grafu je právě konstanta a nezávisle proměnnou. Zvolíme nějakou počáteční podmínku z intervalu (0;1) a vynecháme velký počet (100-10000) iterací funkce gⁿ(x), tím se chování ustálí a potom začneme vykreslovat hodnoty gⁿ(x). Objeví se tolik bodů nad sebou, kolika bodový kanál daná mapa má. Pro dostatečně jemné krokování konstanty a body splynou ve spojité čáry.

Doposud všechny uvedené funkce směřovaly k nějakému rovnovážnému stavu, přestože někdy dlouho a chaoticky. Jedním z hlavních rysů chaosu je ovšem citlivost na počáteční podmínky. Proto zde uvedu ještě jednu funkci, které tuto vlastnost demonstruje. Představte si funkci f(x)=3x-[3x] (desetinná část z 3x). Myslím, že vše vyplyne z následující tabulky.