archimédes
Archimédes patří spolu s Newtonem a Guassem mezi tři nejvýznamnější matematiky všech dob. V době, kdy žil, což bylo asi v letech 287 - 212 př.n.l., byl znám jako “mudrc”, “mistr” či “velký geometr”, přesto tehdy nebyl plně doceněn. Význam jeho života a př
ínos pro vědu můžeme ocenit až nyní.Byl synem astronoma Phidia a historicky je doložen i rok jeho násilné smrti. Celý život až na studia v Euklidově škole v Alexandrii prožil v Syrakusách, řecké námořní kolonii na Sicílii. Brzy se stal skutečným mistrem ve znalostech tehdejší matematiky a začal se zabývat novými problémy, při jejichž řešení prý zapomínal i jíst. Neměl možnost používat tabuli či papír, tak k nákresům svých geometrických obrazců užíval všechno možné: od písku a prachu na zemi, přes popel z ohně až po malování náčrtků v olivovém oleji, který zůstal po koupeli na jeho těle. To vysvětluje malé množství jeho myšlenek, které zůstaly zachovány. Vše, co se dochovalo, jsou jeho dopisy, tzv. poselství Eratosthenovi, Kononovi a Dosifeovi. Zkonstruoval řadu mechanických obranných prostředků, které udivovaly svou údernou silou a možnostmi celý tehdejší svět, jenž byl právě dějištěm punských válek Římanů s Kartágem, pro Archimeda však velký význam neměly. Nebyl na ně natolik hrdý, aby mu stálo zato zmíni
t se o nich ve svých poselstvech velkým matematikům, proto jak vypadala konstrukce těchto strojů se můžeme jen domnívat.Do údobí Archimédova života spadá přesun těžiště řecké kultury a vzdělanosti z oblasti filozofie (6. až 4. století př.n.l.) do oblasti přírodních věd, a to především do matematiky, mechaniky a astronomie. Archimédes navázal za svého života úzký kontakt s tehdejším střediskem vzdělanosti - Alexandrii, především s matematikem Kononem a Eratosthenem. K jeho slávě velkou měrou přispělo jeho přátelství s Hieronem, tehdejším králem Syrakus, a Gelonem, Hieronovým synem. Historické prameny se shodují v tom, že byl výjimečným člověkem, jemuž nebylo zatěžko rozřešit “zda je Země připevněna ke své ose, nebo zda se otáčí , “proč voda rozlitá po celém povrchu Země přilne k jejímu povrchu , “proč má Měsíc různé fáze , “jakému zákonu podléhá příliv a odliv” . Rovněž známé je i jeho úspěšné řešení problému zda Hieronovu korunu vyrobili zlatníci z ryzího zlata nebo jen ze slitiny zlata a stříbra.
Podle úda
jů, které dnes máme k dispozici, usuzujeme, že svá díla napsal až po dosažení 40. roku věku, podle obsahu jednotlivých prací rozdělujeme jeho činnost do čtyř období:I. Období inženýrské činnosti - zavedení pojmu těžiště a určení polohy těžiště pro nejjednodušší rovinné obrazce a tělesa.
II. Období určování obsahů rovinných geometrických obrazců a objemů geometrických těles.
III. Období řešení úloh matematické fyziky.
Do prvních dvou období jeho činnosti zařazujeme
následující díla:a) Kvadratura paraboly,
b) 0 kouli a válci,
c) 0 spirálách,
d) 0 konoidech a aféroidech.
Díla jsou psána formou dopisů Dosifeovi.
Ke třetímu období patří jeho práce:
e) 0 rovnováze rovinných útvarů,
f) 0 mechanických větách (uvedeno jako dopis Eratosthenovi),
g) 0 plovoucích tělesech.
K poslednímu období patří práce:
h) Měření kruhu,
i) 0 počtu písečných zrn.
Archimédova díla se zachovala jen v arabských a jiných přepisech a překladech. Pravděpodobně byl autorem i dalších prací, např. 0 kruhu, 0 trojúhelnících, Katoptrika (odraz světla), 0 sedmiúhelníku v kruhu, O polopravidelných mnohoúhelnících atd.
V prvních čtyřech dílech a) až d) rozvinul Archimédes Eudoxovu metodu výpočtu obsahu nepravidelného obrazce vepisováním pravidelných mnohoúhelníků se stále větším počtem stran. Uvažoval o vepsaných i opsaných mnohoúhelnících a na základě svých úvah určil metodou mechanické kvadratury hodnoty součtů (dnes určitých integrálů) při výpočtu povrchu koule nebo při výpočtu plochy ohraničené spirálou. Stejnou metodou určil i objemy úsečí rotačního paraboloidu, elipsoidu a hyperboloidu. V jeho dílech se již objevují některé základní myšlenky později vytvořeného diferenciálního počtu.
Díla, která Archimédes vytvořil ve třetím období svého života, jsou z hlediska fyziky nejcennější. Vrátil se v nich k fyzikálním problémům, které řešil pomocí matematiky, především úměrami. Vypracoval teorii páky, vypočítal polohu těžiště pro rotační plochy a z ní stanovil podmínky pro stabilní rovnovážnou polohu rotačního paraboloidu plovoucího na kapalině.
V posledním období svého života řešil problémy jak popsat geometrické veličiny užitím čísel. Vytvořil také systém pro zapisování velkých čísel. V díle 0 počtu písečných zrn došel podle dnešních značení k číslu 1063, což byl počet písečných zrn, která podle něho vyplňovala celý tehdy známý vesmír.
Je zřejmé, že Archimédes byl velký vědec, proto vysvětlit všechny jeho myšlenky v jedné práci je nemožné. Jeho důvtipný styl si však můžeme demonstrovat alespoň na jedné uká
zce z jeho díla:Kvadratura paraboly
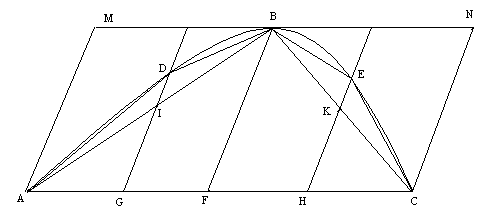
V Poselství Eratosthenovi o mechanických větách Archimédes poprvé uvádí svůj poznatek o velikosti obsahu úseče paraboly, který objevil pomocí mechaniky, a to, že každá úseč paraboly vytváří čtyři třetiny trojúhelníku s touž základnou a stejnou výškou. Před větou, která obsahuje geometrický důkaz tohoto tvrzení, jsou věty, které stručně vysvětlím.
Trojúhelník je po
základnou AC s ní rovnoběžnou; AM, CN jsou rovnoběžné s průměrem BF paraboly. Tvrzení věty je zřejmé z toho, že úseč je menší než rovnoběžník AMNC.
Tento poznatek lze přenést na trojúhelníky a úseče ADB, BEC sestrojené pomocí průměrů ID, KE rovnoběžných s FB.

Trojúhelník ABC je prvním útvarem vepsaným do úseče ABC; druhým je sjednocení trojúhelníků ABC, ADB, BEC; třetí se získá připojením dalších trojúhelníků se základnami AD, DB, BE, EC atd. Pro obsahy těchto útvarů platí:
III. Vezmeme-li jakýkoliv počet ploch tvořících spojitou proporci v poměru 4:1, přičemž největší se rovná trojúhelníku vepsanému do úseče, pak všechny tyto plochy dohromady budou menší než úseč.
Archimédes důvtipně vytvořil geometrickou řadu s kvocientem 1/4, o jejímž částečném součtu odvodil větu:
To platí pro jakékoliv konečné přirozené
n včetně 0. Dále Archimédes užívá Euduxovy exhaustivní metody uvedené v 10. knize Eukleidových Základů a dospívá k výsledku, ke kterému bychom došli užitím limity. Poroste-li totiž n do nekonečna, budeS = a. lim S (1/4)k (suma je od k=0 do n)
a po vyřešení této jednoduché limity posloupnosti nám vyjde, že S = 4/3.a
.
K důkazu věty použiji Archimédova textu v dopise Eratosthenovi:
Nechť ADBEC je úseč sevřená mezi přímkou a parabolou, ABC je trojúhelník mající s úsečí společnou základnu a stejnou výšku. Nechť plocha K tvoří čtyři třetiny trojúhelníku ABC. Je třeba dokázat, že tato plocha se rovná úseči ADBEC, což nejlépe půjde sporem. Když se nerovná, bude buďto větší nebo menší.
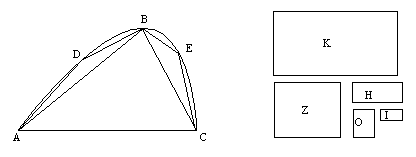
2. Nechť nyní, je-li to možné, bude úseč menší než K. Vezměme plochu Z rovnou trojúhelníku ABC, potom plochu H rovnou čtvrtině Z, dále O rovnou čtvrtině H a takto budeme brát stále ve spojité proporci až do doby, kdy se poslední plocha ukáže být menší než ten rozdíl, o který je plocha K větší než úseč ADBEC. Nechť tato menší plocha je I; tehdy plochy Z, H, O, I dohromady spolu s třetinou I tvoří čtyři třetiny Z (podle věty IV.). Ale K také tvoří čtyři třetiny Z; to znamená, že K bude rovna plochám Z, H, O, I vzatým spolu s třetinou I. Protože plocha K je větší než plochy Z, H, O, I
o veličinu menší než I, ale úseč ADBEC je větší o veličinu větší než I, je jasné, že plochy Z, H, O, I budou větší než úseč. To je nemožné, protože je dokázáno (věta III.), že když se vezme libovolný počet ploch tvořících spojitou proporci v poměru 4:1, přičemž největší se rovná trojúhelníku vepsanému do úseče, pak všechny tyto plochy dohromady budou menší než úseč; to znamená, že úseč ADBEC není menší než plocha K. Ale je také dokázáno, že nebude ani větší; to znamená, že se bude rovnat ploše K. Ale plocha K tvoří čtyři třetiny trojúhelníku ABC; to znamená, že úseč ADBEC se rovná čtyřem třetinám trojúhelníku ABC.Tento jeho důkaz není nic jiného nežli praktické užití Eudoxovy metody. Vyšetřovanou míru S (obsah úseče ADBEC) aproximuje dvěma posloupnostmi a
n , bn s kladnými členy tak, že pro každé přirozené n platí an<S<bn; hodnotu K (z dnešního hlediska jde o společnou limitu uvedených posloupností) bere z odhadu a rovnost S=K dokazuje tím, že od předpokladů S<K, S>K dojde ke sporům (zpravidla k důsledkům, že pro některé n platí bn<K či an>K).